If
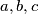
are three positive real numbers such that
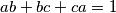
, prove that
![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
%V0
If $a, b, c$ are three positive real numbers such that $ab+bc+ca = 1$, prove that $$\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.$$