Neka su u tetraedru

površina strana

,

,
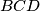
i
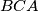
redom jednake
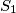
,
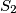
,
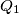
,
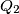
, a prostorni kut između strana

i

jednak

, odnosno

između
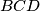
i
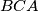
. Dokažite da je
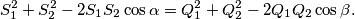
%V0
Neka su u tetraedru $ABCD$ površina strana $ABD$, $ACD$, $BCD$ i $BCA$ redom jednake $S_1$, $S_2$, $Q_1$, $Q_2$, a prostorni kut između strana $ABD$ i $ACD$ jednak $\alpha$, odnosno $\beta$ između $BCD$ i $BCA$. Dokažite da je $$S_1^2 + S_2^2 - 2S_1S_2\cos \alpha = Q_1^2 + Q_2^2 - 2Q_1Q_2\cos \beta \text{.}$$