The function

from the set
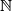
of positive integers into itself is defined by the equality
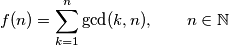
a) Prove that
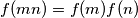
for every two relatively prime
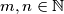
.
b) Prove that for each
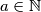
the equation
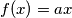
has a solution.
c) Find all
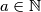
such that the equation
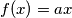
has a unique solution.
%V0
The function $f$ from the set $\mathbb{N}$ of positive integers into itself is defined by the equality
$$\displaystyle f(n)=\sum_{k=1}^{n} \gcd(k,n),\qquad n\in \mathbb{N}$$
a) Prove that $f(mn)=f(m)f(n)$ for every two relatively prime ${m,n\in\mathbb{N}}$.
b) Prove that for each $a\in\mathbb{N}$ the equation $f(x)=ax$ has a solution.
c) Find all $a \in \mathbb{N}$ such that the equation $f(x)=ax$ has a unique solution.