Slični zadaci
Let 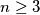 be a fixed integer. Each side and each diagonal of a regular
be a fixed integer. Each side and each diagonal of a regular  -gon is labelled with a number from the set
-gon is labelled with a number from the set 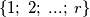 in a way such that the following two conditions are fulfilled:
in a way such that the following two conditions are fulfilled:
1. Each number from the set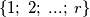 occurs at least once as a label.
occurs at least once as a label.
2. In each triangle formed by three vertices of the -gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
-gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
(a) Find the maximal for which such a labelling is possible.
for which such a labelling is possible.
(b) Harder version (IMO Shortlist 2005): For this maximal value of , how many such labellings are there?
, how many such labellings are there?
Easier version (5th German TST 2006) - contains answer to the harder versionEasier version (5th German TST 2006): Show that, for this maximal value of , there are exactly
, there are exactly 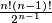 possible labellings.
possible labellings.
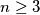 be a fixed integer. Each side and each diagonal of a regular
be a fixed integer. Each side and each diagonal of a regular  -gon is labelled with a number from the set
-gon is labelled with a number from the set 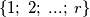 in a way such that the following two conditions are fulfilled:
in a way such that the following two conditions are fulfilled: 1. Each number from the set
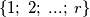 occurs at least once as a label.
occurs at least once as a label. 2. In each triangle formed by three vertices of the
 -gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
-gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side. (a) Find the maximal
 for which such a labelling is possible.
for which such a labelling is possible. (b) Harder version (IMO Shortlist 2005): For this maximal value of
 , how many such labellings are there?
, how many such labellings are there? Easier version (5th German TST 2006) - contains answer to the harder versionEasier version (5th German TST 2006): Show that, for this maximal value of
 , there are exactly
, there are exactly 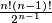 possible labellings.
possible labellings. Let  be an acute-angled triangle with
be an acute-angled triangle with 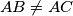 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 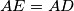 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 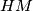 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 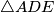 .
.
 be an acute-angled triangle with
be an acute-angled triangle with 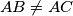 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 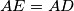 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 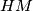 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 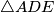 .
. Let  be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let  be the incircle of triangle
be the incircle of triangle  . The median
. The median  of triangle
of triangle  intersects the incircle
intersects the incircle  at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle  again in two points
again in two points  and
and  . Let the lines
. Let the lines 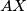 and
and 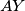 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 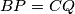 .
.
 be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let  be the incircle of triangle
be the incircle of triangle  . The median
. The median  of triangle
of triangle  intersects the incircle
intersects the incircle  at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle  again in two points
again in two points  and
and  . Let the lines
. Let the lines 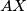 and
and 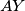 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 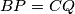 .
.  Školjka
Školjka  be a parallelogram. A variable line
be a parallelogram. A variable line  through the vertex
through the vertex  intersects the rays
intersects the rays 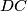 at the points
at the points 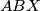 and
and 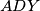 . Show that the angle
. Show that the angle 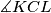 is independent of the line
is independent of the line 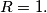 Let
Let  be the inradius of the orthic triangle
be the inradius of the orthic triangle 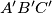 of triangle
of triangle  Prove that
Prove that 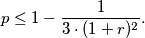
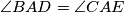 . If
. If  are, respectively, the points of tangency of the incircles of the triangles
are, respectively, the points of tangency of the incircles of the triangles 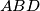 and
and 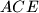 with the line
with the line 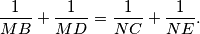
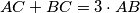 . The incircle of triangle
. The incircle of triangle  and touches the sides
and touches the sides  at the points
at the points  ,
,