Let  be an acute-angled triangle with
be an acute-angled triangle with 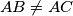 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 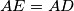 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 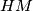 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 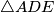 .
.
 be an acute-angled triangle with
be an acute-angled triangle with 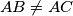 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 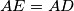 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 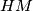 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 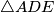 .
. Slični zadaci
Let  be an isosceles triangle with
be an isosceles triangle with 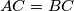 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 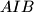 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 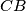 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 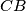 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 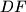 and
and 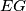 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
.
comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
 be an isosceles triangle with
be an isosceles triangle with 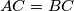 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 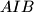 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 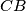 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 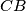 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 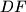 and
and 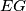 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
. comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
Let  be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let  be the incircle of triangle
be the incircle of triangle  . The median
. The median  of triangle
of triangle  intersects the incircle
intersects the incircle  at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle  again in two points
again in two points  and
and  . Let the lines
. Let the lines 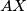 and
and 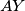 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 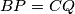 .
.
 be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let  be the incircle of triangle
be the incircle of triangle  . The median
. The median  of triangle
of triangle  intersects the incircle
intersects the incircle  at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle  again in two points
again in two points  and
and  . Let the lines
. Let the lines 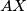 and
and 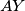 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 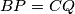 .
. Let  be a fixed triangle, and let
be a fixed triangle, and let  ,
,  ,
,  be the midpoints of sides
be the midpoints of sides  ,
,  ,
,  , respectively. Let
, respectively. Let  be a variable point on the circumcircle. Let lines
be a variable point on the circumcircle. Let lines 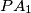 ,
, 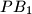 ,
, 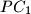 meet the circumcircle again at
meet the circumcircle again at 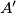 ,
, 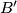 ,
, 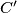 , respectively. Assume that the points
, respectively. Assume that the points  ,
,  ,
,  ,
, 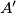 ,
, 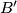 ,
, 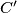 are distinct, and lines
are distinct, and lines 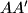 ,
, 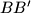 ,
, 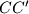 form a triangle. Prove that the area of this triangle does not depend on
form a triangle. Prove that the area of this triangle does not depend on  .
.
Author: Christopher Bradley, United Kingdom
 be a fixed triangle, and let
be a fixed triangle, and let  ,
,  ,
,  be the midpoints of sides
be the midpoints of sides  ,
,  ,
,  , respectively. Let
, respectively. Let  be a variable point on the circumcircle. Let lines
be a variable point on the circumcircle. Let lines 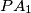 ,
, 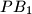 ,
, 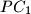 meet the circumcircle again at
meet the circumcircle again at 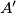 ,
, 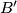 ,
, 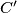 , respectively. Assume that the points
, respectively. Assume that the points  ,
,  ,
,  ,
, 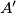 ,
, 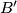 ,
, 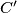 are distinct, and lines
are distinct, and lines 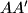 ,
, 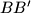 ,
, 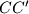 form a triangle. Prove that the area of this triangle does not depend on
form a triangle. Prove that the area of this triangle does not depend on  .
. Author: Christopher Bradley, United Kingdom
 Školjka
Školjka  be a parallelogram. A variable line
be a parallelogram. A variable line  through the vertex
through the vertex 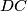 at the points
at the points 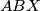 and
and 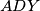 . Show that the angle
. Show that the angle 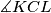 is independent of the line
is independent of the line  be the feet of the perpendiculars from the points
be the feet of the perpendiculars from the points  ,
, 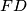 ,
, 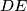 , respectively.
, respectively. 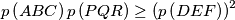 , where
, where 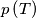 denotes the perimeter of triangle
denotes the perimeter of triangle  .
. 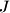 be the center of the excircle tangent to side
be the center of the excircle tangent to side 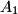 and to the extensions of the sides
and to the extensions of the sides 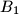 and
and 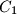 respectively. Suppose that the lines
respectively. Suppose that the lines 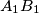 and
and 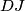 . Determine the angles
. Determine the angles 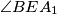 and
and 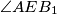 .
.