Slični zadaci
A circle  bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively).
Show that are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points.
Original Statement:
A circle is said to cut a circle
is said to cut a circle 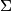 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 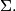
Let be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 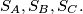
 bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively). Show that
 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points. Original Statement:
A circle
 is said to cut a circle
is said to cut a circle 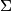 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 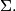
Let
 be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 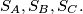
Let  be a finite set of points in the plane such that no three of them are on a line. For each convex polygon
be a finite set of points in the plane such that no three of them are on a line. For each convex polygon  whose vertices are in
whose vertices are in  , let
, let 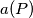 be the number of vertices of
be the number of vertices of  , and let
, and let 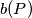 be the number of points of
be the number of points of  which are outside
which are outside  . A line segment, a point, and the empty set are considered as convex polygons of
. A line segment, a point, and the empty set are considered as convex polygons of  ,
,  , and
, and  vertices respectively. Prove that for every real number
vertices respectively. Prove that for every real number  :
:
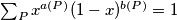 , where the sum is taken over all convex polygons with vertices in
, where the sum is taken over all convex polygons with vertices in  .
.
Alternative formulation:
Let be a finite point set in the plane and no three points are collinear. A subset
be a finite point set in the plane and no three points are collinear. A subset  of
of  will be called round if its elements is the set of vertices of a convex
will be called round if its elements is the set of vertices of a convex 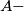 gon
gon 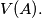 For each round subset let
For each round subset let 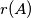 be the number of points from
be the number of points from  which are exterior from the convex
which are exterior from the convex 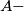 gon
gon 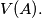 Subsets with
Subsets with 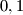 and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset
and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset  of
of  construct the polynomial
construct the polynomial
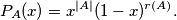
Show that the sum of polynomials for all round subsets is exactly the polynomial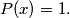
 be a finite set of points in the plane such that no three of them are on a line. For each convex polygon
be a finite set of points in the plane such that no three of them are on a line. For each convex polygon  whose vertices are in
whose vertices are in  , let
, let 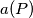 be the number of vertices of
be the number of vertices of  , and let
, and let 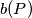 be the number of points of
be the number of points of  which are outside
which are outside  . A line segment, a point, and the empty set are considered as convex polygons of
. A line segment, a point, and the empty set are considered as convex polygons of  ,
,  , and
, and  vertices respectively. Prove that for every real number
vertices respectively. Prove that for every real number  :
: 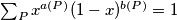 , where the sum is taken over all convex polygons with vertices in
, where the sum is taken over all convex polygons with vertices in  .
. Alternative formulation:
Let
 be a finite point set in the plane and no three points are collinear. A subset
be a finite point set in the plane and no three points are collinear. A subset  of
of  will be called round if its elements is the set of vertices of a convex
will be called round if its elements is the set of vertices of a convex 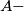 gon
gon 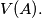 For each round subset let
For each round subset let 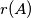 be the number of points from
be the number of points from  which are exterior from the convex
which are exterior from the convex 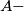 gon
gon 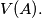 Subsets with
Subsets with 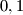 and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset
and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset  of
of  construct the polynomial
construct the polynomial 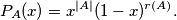
Show that the sum of polynomials for all round subsets is exactly the polynomial
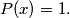
A cake has the form of an  x
x  square composed of
square composed of 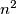 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
.
Prove that arrangement can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
 x
x  square composed of
square composed of 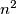 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
. Prove that arrangement
 can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle. Given trapezoid  with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 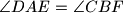 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 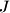 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 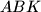 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 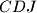 .
.
Proposed by Charles Leytem, Luxembourg
 with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 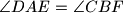 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 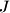 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 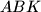 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 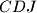 .
. Proposed by Charles Leytem, Luxembourg
 Školjka
Školjka  be a trapezoid with parallel sides
be a trapezoid with parallel sides 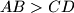 . Points
. Points  lie on the line segments
lie on the line segments 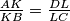 . Suppose that there are points
. Suppose that there are points  on the line segment
on the line segment 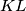 satisfying
satisfying 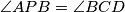 and
and 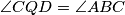 . Prove that the points
. Prove that the points  are concylic.
are concylic. 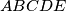 such that
such that 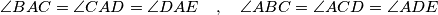
 and
and 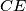 . Prove that the line
. Prove that the line 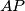 passes through the midpoint of the side
passes through the midpoint of the side