Points 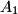 ,
, 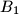 ,
, 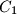 are chosen on the sides
are chosen on the sides  ,
,  ,
,  of a triangle
of a triangle  respectively. The circumcircles of triangles
respectively. The circumcircles of triangles 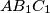 ,
, 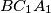 ,
, 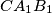 intersect the circumcircle of triangle
intersect the circumcircle of triangle  again at points
again at points 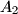 ,
, 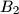 ,
, 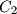 respectively (
respectively (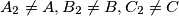 ). Points
). Points 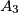 ,
, 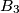 ,
, 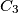 are symmetric to
are symmetric to 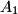 ,
, 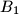 ,
, 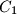 with respect to the midpoints of the sides
with respect to the midpoints of the sides  ,
,  ,
,  respectively. Prove that the triangles
respectively. Prove that the triangles 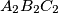 and
and 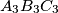 are similar.
are similar.
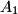 ,
, 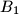 ,
, 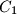 are chosen on the sides
are chosen on the sides  ,
,  ,
,  of a triangle
of a triangle  respectively. The circumcircles of triangles
respectively. The circumcircles of triangles 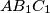 ,
, 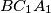 ,
, 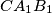 intersect the circumcircle of triangle
intersect the circumcircle of triangle  again at points
again at points 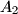 ,
, 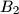 ,
, 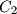 respectively (
respectively (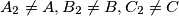 ). Points
). Points 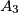 ,
, 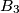 ,
, 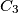 are symmetric to
are symmetric to 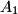 ,
, 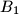 ,
, 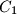 with respect to the midpoints of the sides
with respect to the midpoints of the sides  ,
,  ,
,  respectively. Prove that the triangles
respectively. Prove that the triangles 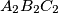 and
and 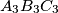 are similar.
are similar.  Školjka
Školjka