Let

be a polynomial of degree
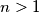
with integer coefficients and let

be a positive integer. Consider the polynomial
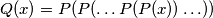
, where

occurs

times. Prove that there are at most

integers

such that
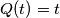
.
%V0
Let $P(x)$ be a polynomial of degree $n > 1$ with integer coefficients and let $k$ be a positive integer. Consider the polynomial $Q(x) = P(P(\ldots P(P(x)) \ldots ))$, where $P$ occurs $k$ times. Prove that there are at most $n$ integers $t$ such that $Q(t) = t$.