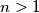
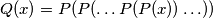
Let be a polynomial of degree with integer coefficients and let be a positive integer. Consider the polynomial , where occurs times. Prove that there are at most integers such that .
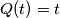
%V0
Let $P(x)$ be a polynomial of degree $n > 1$ with integer coefficients and let $k$ be a positive integer. Consider the polynomial $Q(x) = P(P(\ldots P(P(x)) \ldots ))$, where $P$ occurs $k$ times. Prove that there are at most $n$ integers $t$ such that $Q(t) = t$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
be a polynomial of degree 
with integer coefficients and let 
be a positive integer. Consider the polynomial 
, where 
occurs 
integers 
such that 
.