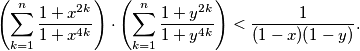Slični zadaci
For  and
and 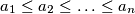 given real numbers we have the following instructions:
given real numbers we have the following instructions:
- place out the numbers in some order in a ring;
- delete one of the numbers from the ring;
- if just two numbers are remaining in the ring: let be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
Afterwards start again with the step (2). Show that the largest sum which can result in this way is given by the formula
which can result in this way is given by the formula
![S_{max}= \sum^n_{k=2} \begin{pmatrix} n -2 \\ [\frac{k}{2}] - 1\end{pmatrix}a_{k}.](/media/m/a/d/4/ad4e65bc42b08da06d18502a103d6a04.png)
 and
and 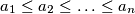 given real numbers we have the following instructions:
given real numbers we have the following instructions: - place out the numbers in some order in a ring;
- delete one of the numbers from the ring;
- if just two numbers are remaining in the ring: let
 be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace Afterwards start again with the step (2). Show that the largest sum
 which can result in this way is given by the formula
which can result in this way is given by the formula ![S_{max}= \sum^n_{k=2} \begin{pmatrix} n -2 \\ [\frac{k}{2}] - 1\end{pmatrix}a_{k}.](/media/m/a/d/4/ad4e65bc42b08da06d18502a103d6a04.png)
Consider two monotonically decreasing sequences 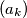 and
and  , where
, where 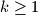 , and
, and 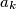 and
and 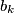 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences
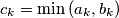 ;
;
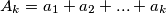 ;
;
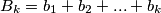 ;
;
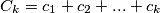
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences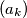 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 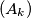 and
and 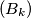 are not bounded, while the sequence
are not bounded, while the sequence 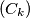 is bounded?
is bounded?
(b) Does the answer to problem (a) change if we stipulate that the sequence must be
must be 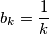 for all k ?
for all k ?
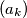 and
and  , where
, where 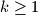 , and
, and 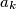 and
and 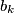 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences 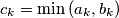 ;
; 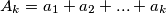 ;
; 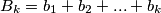 ;
; 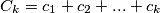
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences
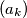 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 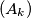 and
and 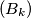 are not bounded, while the sequence
are not bounded, while the sequence 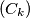 is bounded?
is bounded? (b) Does the answer to problem (a) change if we stipulate that the sequence
 must be
must be 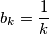 for all k ?
for all k ?  Školjka
Školjka 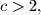 and let
and let 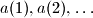 be a sequence of nonnegative real numbers such that
be a sequence of nonnegative real numbers such that 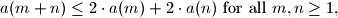
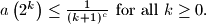 Prove that the sequence
Prove that the sequence 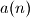 is bounded.
is bounded. 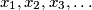 are positive real numbers for which
are positive real numbers for which 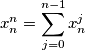 for
for 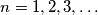 Prove that
Prove that 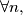
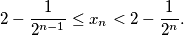
 be a positive integer and let
be a positive integer and let 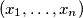 ,
, 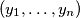 be two sequences of positive real numbers. Suppose
be two sequences of positive real numbers. Suppose 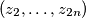 is a sequence of positive real numbers such that
is a sequence of positive real numbers such that 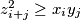 for all
for all 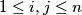 .
. 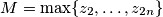 . Prove that
. Prove that 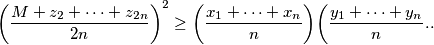
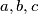 are three positive real numbers such that
are three positive real numbers such that 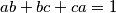 , prove that
, prove that ![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
 and
and  be a positive real number such that
be a positive real number such that 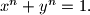 Prove that
Prove that