Neka su

i

pozitivni iracionalni brojevi takvi da je
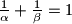
, te
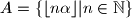
i
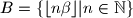
. Dokažite da je tada
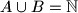
i
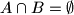
.
Naputak: Možete dokazati ekvivalentnu tvrdnju: Za funkciju
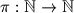
definiranu sa
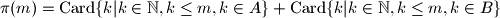
vrijedi
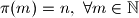
.
(
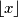
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Neka su $\alpha$ i $\beta$ pozitivni iracionalni brojevi takvi da je $\frac1\alpha + \frac1\beta = 1$, te $A=\{\lfloor n\alpha \rfloor | n \in \mathbb{N}\}$ i $B=\{\lfloor n\beta \rfloor | n \in \mathbb{N}\}$. Dokažite da je tada $A \cup B = \mathbb{N}$ i $A \cap B = \emptyset$.
Naputak: Možete dokazati ekvivalentnu tvrdnju: Za funkciju $\pi : \mathbb{N} \rightarrow \mathbb{N}$ definiranu sa
$$\pi(m)=\mathrm{Card} \{k | k \in \mathbb{N}, k \leq m, k \in A\} + \mathrm{Card} \{k | k \in \mathbb{N}, k \leq m, k \in B\}$$ vrijedi $\pi(m)=n, \,\, \forall m \in \mathbb{N}$.
( $\lfloor x \rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)