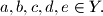Find all positive integers  for which the numbers in the set
for which the numbers in the set 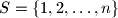 can be colored red and blue, with the following condition being satisfied: The set
can be colored red and blue, with the following condition being satisfied: The set 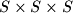 contains exactly
contains exactly 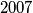 ordered triples
ordered triples 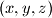 such that:
such that:
(i) the numbers ,
,  ,
,  are of the same color,
are of the same color,
and
(ii) the number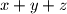 is divisible by
is divisible by  .
.
Author: Gerhard Wöginger, Netherlands
 for which the numbers in the set
for which the numbers in the set 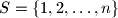 can be colored red and blue, with the following condition being satisfied: The set
can be colored red and blue, with the following condition being satisfied: The set 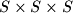 contains exactly
contains exactly 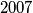 ordered triples
ordered triples 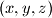 such that:
such that: (i) the numbers
 ,
,  ,
,  are of the same color,
are of the same color, and
(ii) the number
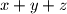 is divisible by
is divisible by  .
. Author: Gerhard Wöginger, Netherlands
Slični zadaci
Show that for any finite set  of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
.
Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
 of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
. Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
Let  be a positive integer. A sequence of
be a positive integer. A sequence of  positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer
positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer 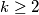 , if the number
, if the number  appears in the sequence then so does the number
appears in the sequence then so does the number 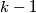 , and moreover the first occurrence of
, and moreover the first occurrence of 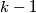 comes before the last occurrence of
comes before the last occurrence of  . For each
. For each  , how many full sequences are there ?
, how many full sequences are there ?
 be a positive integer. A sequence of
be a positive integer. A sequence of  positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer
positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer 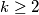 , if the number
, if the number  appears in the sequence then so does the number
appears in the sequence then so does the number 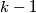 , and moreover the first occurrence of
, and moreover the first occurrence of 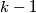 comes before the last occurrence of
comes before the last occurrence of  . For each
. For each  , how many full sequences are there ?
, how many full sequences are there ? Let  be the set of ordered triples
be the set of ordered triples 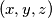 , where
, where 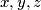 are integers with
are integers with 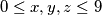 . Players
. Players  and
and  play the following guessing game. Player
play the following guessing game. Player  chooses a triple
chooses a triple 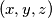 in
in  , and Player
, and Player  has to discover
has to discover  's triple in as few moves as possible. A move consists of the following:
's triple in as few moves as possible. A move consists of the following:  gives
gives  a triple
a triple 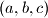 in
in  , and
, and  replies by giving
replies by giving  the number
the number 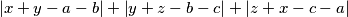 . Find the minimum number of moves that
. Find the minimum number of moves that  needs to be sure of determining
needs to be sure of determining  's triple.
's triple.
 be the set of ordered triples
be the set of ordered triples 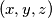 , where
, where 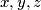 are integers with
are integers with 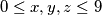 . Players
. Players  and
and  play the following guessing game. Player
play the following guessing game. Player  chooses a triple
chooses a triple 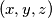 in
in  , and Player
, and Player  has to discover
has to discover  's triple in as few moves as possible. A move consists of the following:
's triple in as few moves as possible. A move consists of the following:  gives
gives  a triple
a triple 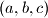 in
in  , and
, and  replies by giving
replies by giving  the number
the number 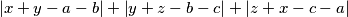 . Find the minimum number of moves that
. Find the minimum number of moves that  needs to be sure of determining
needs to be sure of determining  's triple.
's triple.  Školjka
Školjka 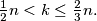 Find the least number
Find the least number  for which it is possible to place
for which it is possible to place 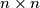 chessboard so that no column or row contains a block of
chessboard so that no column or row contains a block of 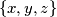 with
with 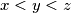 is called historic if
is called historic if 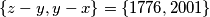 . Show that the set of all nonnegative integers can be written as the union of pairwise disjoint historic sets.
. Show that the set of all nonnegative integers can be written as the union of pairwise disjoint historic sets.  be a set of 10,000 integers, none of them is divisible by 47. Prove that there exists a 2007-element subset
be a set of 10,000 integers, none of them is divisible by 47. Prove that there exists a 2007-element subset  of
of 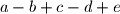 is not divisible by 47 for any
is not divisible by 47 for any