In the Cartesian coordinate plane define the strips 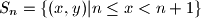 ,
, 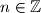 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips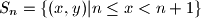 for every integer
for every integer  Assume each strip
Assume each strip 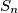 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.
Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
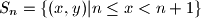 ,
, 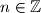 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color. IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips
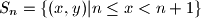 for every integer
for every integer  Assume each strip
Assume each strip 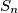 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
 Školjka
Školjka