Slični zadaci
Suppose we have a  -gon. Some
-gon. Some 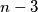 diagonals are coloured black and some other
diagonals are coloured black and some other 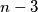 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
.
 -gon. Some
-gon. Some 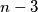 diagonals are coloured black and some other
diagonals are coloured black and some other 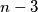 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
. Determine the smallest positive real number  with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points  ,
,  ,
,  , and
, and 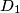 lie on sides
lie on sides  ,
,  ,
,  , and
, and 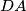 , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 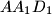 ,
, 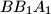 ,
, 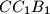 and
and 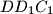 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let  be the area of quadrilateral
be the area of quadrilateral 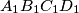 . Then we always have
. Then we always have 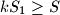 .
.
Author: unknown author, USA
 with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points  ,
,  ,
,  , and
, and 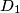 lie on sides
lie on sides  ,
,  ,
,  , and
, and 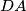 , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 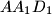 ,
, 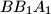 ,
, 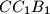 and
and 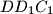 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let  be the area of quadrilateral
be the area of quadrilateral 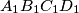 . Then we always have
. Then we always have 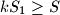 .
. Author: unknown author, USA
 Školjka
Školjka  with
with 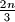 good triangles.
good triangles.  , let
, let  ,
,  ,
,  be the feet of the perpendiculars from the points
be the feet of the perpendiculars from the points  ,
,  ,
,  to the lines
to the lines  ,
,  ,
,  be the feet of the perpendiculars from the points
be the feet of the perpendiculars from the points  ,
, 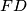 ,
, 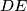 , respectively.
, respectively. 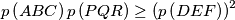 , where
, where 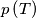 denotes the perimeter of triangle
denotes the perimeter of triangle  .
. 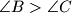 . Point
. Point  is the incenter, and
is the incenter, and  lies on line
lies on line  such that
such that 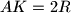 , and
, and 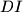 and
and 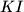 meet sides
meet sides  and
and 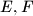 respectively. Let
respectively. Let 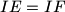 .
. 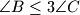 .
.  ,
,  and
and  be the incenters of the triangles
be the incenters of the triangles 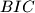 ,
, 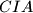 and
and 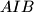 , respectively. Let the triangle
, respectively. Let the triangle 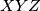 be equilateral. Prove that
be equilateral. Prove that  be a line through
be a line through  and the line
and the line  . Denote by
. Denote by 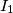 ,
, 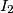 and
and 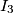 the incenters of
the incenters of 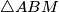 ,
, 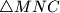 and
and 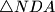 , respectively. Prove that the orthocenter of
, respectively. Prove that the orthocenter of 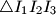 lies on
lies on