Slični zadaci
Let  be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 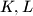 and
and  be the midpoints of the segments
be the midpoints of the segments 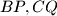 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 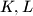 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 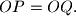
Proposed by Sergei Berlov, Russia
 be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 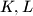 and
and  be the midpoints of the segments
be the midpoints of the segments 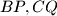 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 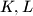 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 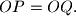
Proposed by Sergei Berlov, Russia
 Školjka
Školjka 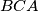 intersects the circumcircle again at
intersects the circumcircle again at  , the perpendicular bisector of
, the perpendicular bisector of  at
at  at
at  and the midpoint of
and the midpoint of  . Prove that the triangles
. Prove that the triangles 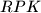 and
and 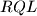 have the same area.
have the same area.  , and let
, and let 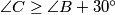 . Prove that
. Prove that 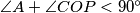 .
. 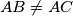 . The circle with diameter
. The circle with diameter  respectively. Denote by
respectively. Denote by 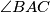 and
and 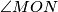 intersect at
intersect at 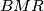 and
and 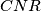 have a common point lying on the side
have a common point lying on the side  . A point
. A point 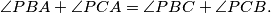 Show that
Show that 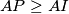 , and that equality holds if and only if
, and that equality holds if and only if 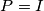 .
.  be the orthocenter of an acute-angled triangle
be the orthocenter of an acute-angled triangle 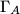 centered at the midpoint of
centered at the midpoint of 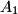 and
and 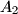 . Similarly, define the points
. Similarly, define the points 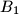 ,
, 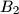 ,
, 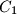 and
and 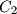 .
. 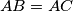 . The angle bisectors of
. The angle bisectors of 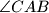 and
and 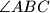 meet the sides
meet the sides 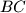 and
and 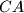 at
at  and
and  , respectively. Let
, respectively. Let 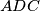 . Suppose that
. Suppose that 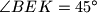 . Find all possible values of
. Find all possible values of