Slični zadaci
a) Show that the set 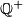 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets.  satisfying the following conditions:
satisfying the following conditions: 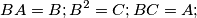 where
where 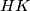 stands for the set
stands for the set 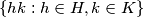 for any two subsets
for any two subsets 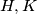 of
of 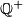 and
and 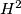 stands for
stands for 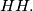
b) Show that all positive rational cubes are in for such a partition of
for such a partition of 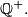
c) Find such a partition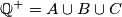 with the property that for no positive integer
with the property that for no positive integer 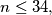 both
both  and
and  are in
are in  that is,
that is, 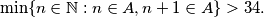
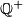 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets.  satisfying the following conditions:
satisfying the following conditions: 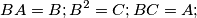 where
where 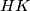 stands for the set
stands for the set 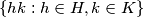 for any two subsets
for any two subsets 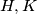 of
of 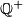 and
and 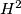 stands for
stands for 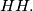
b) Show that all positive rational cubes are in
 for such a partition of
for such a partition of 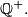
c) Find such a partition
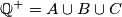 with the property that for no positive integer
with the property that for no positive integer 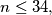 both
both  and
and  are in
are in  that is,
that is, 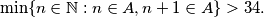
Show that for any finite set  of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
.
Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
 of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
. Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
Consider 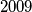 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 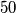 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
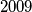 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 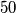 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
 Školjka
Školjka 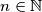 and
and 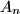 set of all permutations
set of all permutations  of the set
of the set 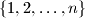 for which
for which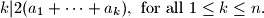
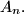
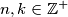 with
with 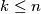 and let
and let 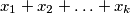 where
where 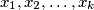 are distinct elements of
are distinct elements of 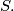 Prove that
Prove that 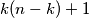 distinct elements.
distinct elements. 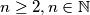 and
and 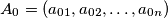 be any
be any 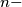 tuple of natural numbers, such that
tuple of natural numbers, such that 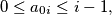 for
for 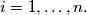
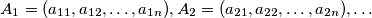 are defined by:
are defined by: 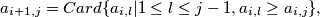 for
for 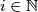 and
and 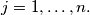 Prove that there exists
Prove that there exists 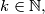 such that
such that 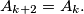
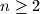 , let
, let 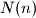 be the maxima number of triples
be the maxima number of triples 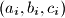 ,
,  , consisting of nonnegative integers
, consisting of nonnegative integers 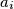 ,
, 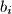 and
and 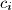 such that the following two conditions are satisfied:
such that the following two conditions are satisfied: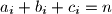 for all
for all 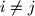 then
then 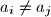 ,
, 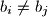 and
and 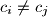 Determine
Determine