For an integer

, denote by
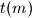
the unique number in
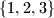
such that
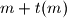
is a multiple of

. A function
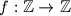
satisfies
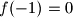
,
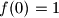
,
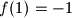
and
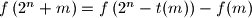
for all integers

,
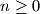
with

. Prove that
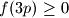
holds for all integers
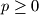
.
Proposed by Gerhard Woeginger, Austria
%V0
For an integer $m$, denote by $t(m)$ the unique number in $\{1, 2, 3\}$ such that $m + t(m)$ is a multiple of $3$. A function $f: \mathbb{Z}\to\mathbb{Z}$ satisfies $f( - 1) = 0$, $f(0) = 1$, $f(1) = - 1$ and $f\left(2^{n} + m\right) = f\left(2^n - t(m)\right) - f(m)$ for all integers $m$, $n\ge 0$ with $2^n > m$. Prove that $f(3p)\ge 0$ holds for all integers $p\ge 0$.
Proposed by Gerhard Woeginger, Austria