Slični zadaci
Let 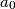 ,
,  ,
,  , ... be an infinite sequence of real numbers satisfying the equation
, ... be an infinite sequence of real numbers satisfying the equation 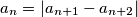 for all
for all 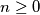 , where
, where 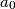 and
and  are two different positive reals.
are two different positive reals.
Can this sequence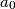 ,
,  ,
,  , ... be bounded?
, ... be bounded?
Remark This one is from the IMO Shortlist 2004, but it's already published on the official BWM website und thus I take the freedom to post it here:
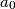 ,
,  ,
,  , ... be an infinite sequence of real numbers satisfying the equation
, ... be an infinite sequence of real numbers satisfying the equation 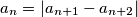 for all
for all 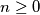 , where
, where 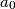 and
and  are two different positive reals.
are two different positive reals. Can this sequence
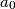 ,
,  ,
,  , ... be bounded?
, ... be bounded? Remark This one is from the IMO Shortlist 2004, but it's already published on the official BWM website und thus I take the freedom to post it here:
 Školjka
Školjka  određeni su cijeli brojevi
određeni su cijeli brojevi  i
i 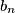 tako da je
tako da je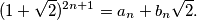
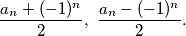
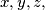 such that :
such that : 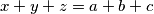
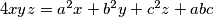
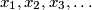 are positive real numbers for which
are positive real numbers for which 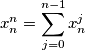 for
for 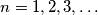 Prove that
Prove that 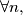
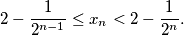
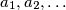 be an infinite sequence of real numbers, for which there exists a real number
be an infinite sequence of real numbers, for which there exists a real number  with
with 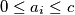 for all
for all  , such that
, such that 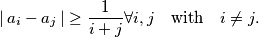
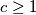 .
. 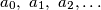 is a sequence of real numbers such that
is a sequence of real numbers such that ![a_{n + 1} = \left[a_{n}\right]\cdot \left\{a_{n}\right\}](/media/m/8/4/1/841a9a2ad06c20187088b2f582b7c6d1.png)
 such that for every
such that for every 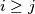 we have
we have 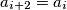 .
. 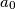 ,
, 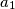 ,
, 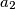 ,
,  be a sequence of reals such that
be a sequence of reals such that 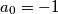 and
and 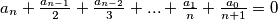 for all
for all 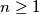 .
. 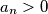 for all
for all