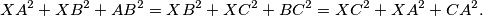Slični zadaci
Let  be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 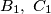 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 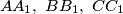 are concurrent.
are concurrent.
 be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 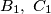 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 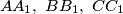 are concurrent.
are concurrent.  Školjka
Školjka  ,
,  ,
,  trokuta
trokuta 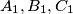 pri čemu se pravci
pri čemu se pravci 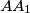 ,
, 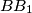 ,
, 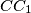 sijeku u jednoj točki. Dokažite da se pravci
sijeku u jednoj točki. Dokažite da se pravci 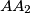 ,
, 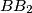 ,
, 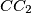 , simetrični danim pravcima u odnosu na odgovarajuće simetrale kutova, također sijeku u jednoj točki.
, simetrični danim pravcima u odnosu na odgovarajuće simetrale kutova, također sijeku u jednoj točki.  na nekoj stranici trokuta
na nekoj stranici trokuta  such that
such that 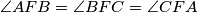 . Let the lines
. Let the lines 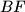 and
and 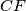 meet the sides
meet the sides  and
and  respectively. Prove that
respectively. Prove that 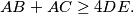
 be an interior point. Prove that
be an interior point. Prove that 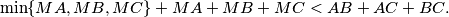
 be a cyclic quadrilateral. Let
be a cyclic quadrilateral. Let  , respectively, such that
, respectively, such that 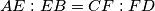 . Let
. Let  such that
such that 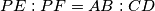 . Prove that the ratio between the areas of triangles
. Prove that the ratio between the areas of triangles 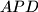 and
and 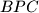 does not depend on the choice of
does not depend on the choice of 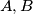 and
and  be non-collinear points. Prove that there is a unique point
be non-collinear points. Prove that there is a unique point  in the plane of
in the plane of