Slični zadaci
The numbers from 1 to 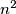 are randomly arranged in the cells of a
are randomly arranged in the cells of a  square (
square ( ). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these
). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these 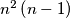 fractions. What is the highest possible value of the characteristic ?
fractions. What is the highest possible value of the characteristic ?
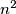 are randomly arranged in the cells of a
are randomly arranged in the cells of a  square (
square ( ). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these
). For any pair of numbers situated on the same row or on the same column the ratio of the greater number to the smaller number is calculated. Let us call the characteristic of the arrangement the smallest of these 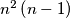 fractions. What is the highest possible value of the characteristic ?
fractions. What is the highest possible value of the characteristic ?  Školjka
Školjka  . Neka je
. Neka je 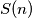 skup kompleksnih brojeva na jediničnoj kružnici u kompleksnoj ravnini sa središtem u točki
skup kompleksnih brojeva na jediničnoj kružnici u kompleksnoj ravnini sa središtem u točki 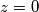 koji zadovoljavaju sljedeću jednakost
koji zadovoljavaju sljedeću jednakost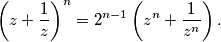
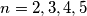 .
.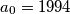 and
and 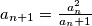 for each nonnegative integer
for each nonnegative integer 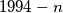 is the greatest integer less than or equal to
is the greatest integer less than or equal to 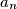 ,
, 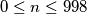
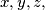 such that :
such that : 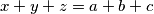
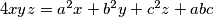
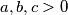 such that
such that 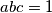 . Prove that
. Prove that 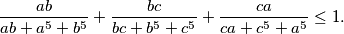
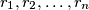 be real numbers greater than or equal to 1. Prove that
be real numbers greater than or equal to 1. Prove that ![\frac{1}{r_{1} + 1} + \frac{1}{r_{2} + 1} + \cdots +\frac{1}{r_{n}+1} \geq \frac{n}{ \sqrt[n]{r_{1}r_{2} \cdots r_{n}}+1}.](/media/m/6/5/9/659a1db9dfb0819c970e78fed531b4ad.png)
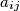 (with the indices
(with the indices  and
and  from the set
from the set 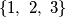 ) be real numbers such that
) be real numbers such that 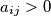 for
for 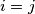 ;
; 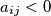 for
for 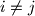 .
. 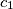 ,
, 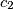 ,
, 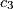 such that the numbers
such that the numbers 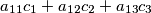 ,
, 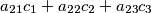 ,
,