Slični zadaci
For an integer 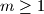 , we consider partitions of a
, we consider partitions of a  chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 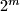 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length  . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.
Proposed by Gerhard Woeginger, Netherlands
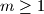 , we consider partitions of a
, we consider partitions of a  chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 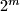 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length  . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.Proposed by Gerhard Woeginger, Netherlands
In the plane we consider rectangles whose sides are parallel to the coordinate axes and have positive length. Such a rectangle will be called a box. Two boxes intersect if they have a common point in their interior or on their boundary. Find the largest  for which there exist
for which there exist  boxes
boxes  ,
,  ,
, 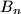 such that
such that 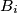 and
and 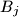 intersect if and only if
intersect if and only if 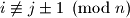 .
.
Proposed by Gerhard Woeginger, Netherlands
 for which there exist
for which there exist  boxes
boxes  ,
,  ,
, 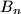 such that
such that 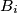 and
and 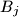 intersect if and only if
intersect if and only if 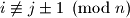 .
. Proposed by Gerhard Woeginger, Netherlands
A rectangle  is partitioned in several (
is partitioned in several (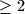 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary.
Author: unknown author, Japan
 is partitioned in several (
is partitioned in several (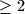 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary. Author: unknown author, Japan
A cake has the form of an  x
x  square composed of
square composed of 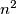 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
.
Prove that arrangement can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
 x
x  square composed of
square composed of 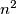 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
. Prove that arrangement
 can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.  Školjka
Školjka 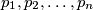 u ravnini su u općem položaju (nikoja dva nisu paralelna i nikoja tri se ne sijeku u istoj točki). Može li se svakom od sjecišta dvaju pravaca pridružiti jedan broj iz skupa
u ravnini su u općem položaju (nikoja dva nisu paralelna i nikoja tri se ne sijeku u istoj točki). Može li se svakom od sjecišta dvaju pravaca pridružiti jedan broj iz skupa 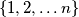 tako da na svakom pravcu budu svi brojevi
tako da na svakom pravcu budu svi brojevi 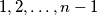 ako je
ako je 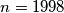 ,
,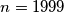 ?
? 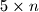 rectangle can be tiled using
rectangle can be tiled using 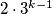 ways to file a fixed
ways to file a fixed 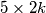 rectangle
rectangle 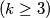 with
with 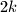 pieces. (symmetric constructions are supposed to be different.)
pieces. (symmetric constructions are supposed to be different.)  be a cyclic quadrilateral. Let
be a cyclic quadrilateral. Let  and
and  be variable points on the sides
be variable points on the sides  and
and  , respectively, such that
, respectively, such that 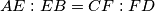 . Let
. Let  be the point on the segment
be the point on the segment  such that
such that 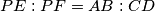 . Prove that the ratio between the areas of triangles
. Prove that the ratio between the areas of triangles 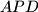 and
and 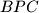 does not depend on the choice of
does not depend on the choice of