U trokutu

dane su točke
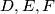
na stranicama

,

,

tako da je
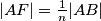
,
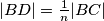
,
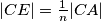
. Pravci
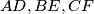
sijeku se u točkama
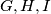
. Pokažite da je površina trokuta
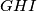
jednaka
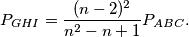
%V0
U trokutu $ABC$ dane su točke $D, E, F$ na stranicama $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ tako da je $|AF|=\frac{1}{n}|AB|$, $|BD|=\frac{1}{n}|BC|$, $|CE|=\frac{1}{n}|CA|$. Pravci $AD, BE, CF$ sijeku se u točkama $G, H, I$. Pokažite da je površina trokuta $GHI$ jednaka
$$ P_{GHI} = \frac{(n-2)^2}{n^2-n+1} P_{ABC} .$$