Slični zadaci
Let  be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 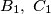 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 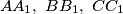 are concurrent.
are concurrent.
 be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 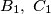 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 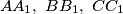 are concurrent.
are concurrent.  Školjka
Školjka 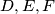 na stranicama
na stranicama 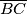 ,
, 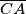 ,
, 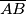 tako da je
tako da je 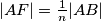 ,
, 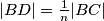 ,
, 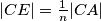 . Pravci
. Pravci 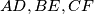 sijeku se u točkama
sijeku se u točkama 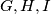 . Pokažite da je površina trokuta
. Pokažite da je površina trokuta 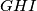 jednaka
jednaka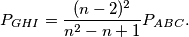
 such that
such that 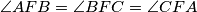 . Let the lines
. Let the lines 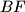 and
and 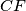 meet the sides
meet the sides  and
and  respectively. Prove that
respectively. Prove that 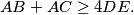
 be an interior point. Prove that
be an interior point. Prove that 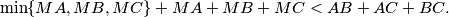
 be a cyclic quadrilateral. Let
be a cyclic quadrilateral. Let  , respectively, such that
, respectively, such that 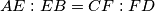 . Let
. Let  be the point on the segment
be the point on the segment  such that
such that 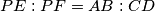 . Prove that the ratio between the areas of triangles
. Prove that the ratio between the areas of triangles 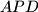 and
and 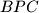 does not depend on the choice of
does not depend on the choice of 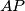 ,
, 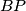 ,
, 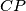 meet the sides
meet the sides  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that 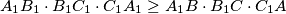 .
.  be the circumcenter and
be the circumcenter and  the orthocenter of an acute-angled triangle
the orthocenter of an acute-angled triangle 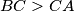 . Let
. Let 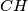 of triangle
of triangle 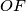 at the point
at the point 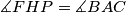 .
.