Given
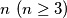
points in space such that every three of them form a triangle with one angle greater than or equal to
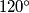
, prove that these points can be denoted by
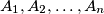
in such a way that for each
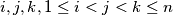
, angle
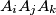
is greater than or equal to
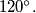
%V0
Given $n \ (n \geq 3)$ points in space such that every three of them form a triangle with one angle greater than or equal to $120^\circ$, prove that these points can be denoted by $A_1,A_2, \ldots,A_n$ in such a way that for each $i, j, k, 1 \leq i < j < k \leq n$, angle $A_iA_jA_k$ is greater than or equal to $120^\circ .$