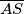
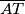
U tetivnom četverokutu je promjer, a središte opisane kružnice. Neka je presjek pravaca i , a presjek i . Dokaži da opisana kružnica trokutu siječe dužine i u polovištima.
%V0
U tetivnom četverokutu $ABCD$ je $\overline{AC}$ promjer, a $O$ središte opisane kružnice. Neka je $S$ presjek pravaca $AD$ i $BC$, a $T$ presjek $AB$ i $CD$. Dokaži da opisana kružnica trokutu $\triangle OBD$ siječe dužine $\overline{AS}$ i $\overline{AT}$ u polovištima.
Školjka 
je 
promjer, a 
središte opisane kružnice. Neka je 
presjek pravaca 
i 
, a 
presjek 
i 
. Dokaži da opisana kružnica trokutu 
siječe dužine 
i 
u polovištima.