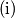
Odredi sve proste brojeve
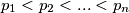
takve da je
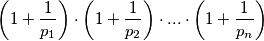
prirodan broj.
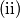
Postoje li prirodni brojevi
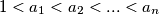
takvi da je
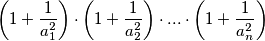
prirodan broj.
%V0
$\text{(i)}$ Odredi sve proste brojeve $p_1<p_2<...<p_n$ takve da je $$\left( 1+\displaystyle\frac{1}{p_1}\right)\cdot \left( 1+\displaystyle \frac{1}{p_2}\right)\cdot ... \cdot \left( 1+\displaystyle\frac{1}{p_n}\right)$$ prirodan broj.
$\text{(ii)}$ Postoje li prirodni brojevi $1<a_1<a_2<...<a_n$ takvi da je $$\left( 1+\displaystyle\frac{1}{a_1^2}\right)\cdot \left( 1+\displaystyle \frac{1}{a_2^2}\right)\cdot ... \cdot \left( 1+\displaystyle\frac{1}{a_n^2}\right)$$ prirodan broj.