Consider a  checkerboard with
checkerboard with 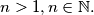 How many possibilities are there to put
How many possibilities are there to put 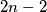 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the  square.
square.
 checkerboard with
checkerboard with 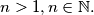 How many possibilities are there to put
How many possibilities are there to put 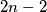 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the  square.
square. Slični zadaci
For each finite set  of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 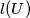 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 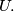 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 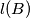 is greater than or equal to
is greater than or equal to 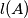 for each nonempty subset
for each nonempty subset  of
of 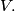
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set consisting of
consisting of 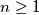 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 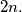
 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 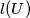 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 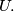 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 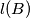 is greater than or equal to
is greater than or equal to 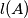 for each nonempty subset
for each nonempty subset  of
of 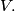
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set
 consisting of
consisting of 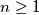 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 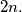
Kiki zamisli dvoznamenkasti broj, a Veki ga pokušava pogoditi. Ako Veki pogodi točan broj ili broj kojemu je jedna znamenka točna a druga se od točne razlikuje za 1 Kiki mu kaže "Toplo!", inače kaže "Hladno!". (npr. ako Kiki zamisli 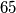 , za pogađane brojeve
, za pogađane brojeve 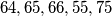 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")
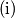 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 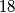 pokušaja.
pokušaja.
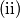 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 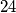 pokušaja.
pokušaja.
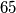 , za pogađane brojeve
, za pogađane brojeve 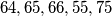 reći će "Toplo!", a za ostale "Hladno!")
reći će "Toplo!", a za ostale "Hladno!")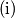 Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od
Dokaži da ne postoji strategija u kojoj Veki sigurno određuje Kikijev broj u ne više od 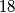 pokušaja.
pokušaja.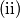 Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od
Pronađite strategiju kojom Veki sigurno određuje Kikijev broj u ne više od 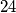 pokušaja.
pokušaja. Roko se šeće po ploči 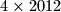 (
( retka,
retka, 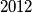 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
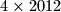 (
( retka,
retka, 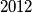 stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?
stupaca), koja je obojana šahovski (polje lijevo gore je crno). Na početku se nalazi na crnom polju u prvom retku i prvom stupcu. U svakom koraku pomakne se prema desno, i to na neko crno polje koje ima jedan vrh zajednički sa poljem na kojem se trenutno nalazi. Na koliko načina se Roko može prošetati pločom i završiti na polju u zadnjem retku i zadnjem stupcu?  Školjka
Školjka 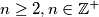 numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers
numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers  for which it is possible to yield
for which it is possible to yield  ,
,  i
i  novčića.
novčića.