Polovištem tetive parabole
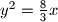
, koja leži na pravcu
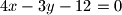
, povučena je paralela s

-osi. Sjecištem te paralele i parabole povučena je na nju tangenta. Pokažite da je ona paralelna sa zadanom tetivom.
%V0
Polovištem tetive parabole $y^2 = \frac{8}{3}x$, koja leži na pravcu $4x - 3y - 12 = 0$, povučena je paralela s $x$-osi. Sjecištem te paralele i parabole povučena je na nju tangenta. Pokažite da je ona paralelna sa zadanom tetivom.