Dan je trokut

i točka

u njegovoj unutrašnjosti. Pravci
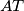
,
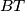
,
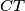
sijeku dužine

,

,

u

,

,

, respektivno. Neka je
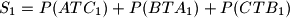
,
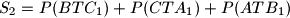
. Dokaži da postoji beskonačno mnogo izbora točke

takvih da je
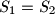
.
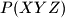
označava provršinu trokuta
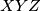
.
%V0
Dan je trokut $ABC$ i točka $T$ u njegovoj unutrašnjosti. Pravci $AT$, $BT$, $CT$ sijeku dužine $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ u $A_1$, $B_1$, $C_1$, respektivno. Neka je $S_1=P(ATC_1)+P(BTA_1)+P(CTB_1)$, $S_2=P(BTC_1)+P(CTA_1)+P(ATB_1)$. Dokaži da postoji beskonačno mnogo izbora točke $T$ takvih da je $S_1=S_2$.
$P(XYZ)$ označava provršinu trokuta $XYZ$.