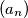
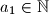
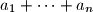
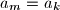
Neka je niz takav da je proizvoljan, a je manji od i takav da je suma djeljiva s . Dokaži da niz nakon nekog člana postane konstantan, tj. postoji takav da je za svaki .
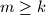
%V0
Neka je $(a_n)$ niz takav da je $a_1 \in \mathbb{N}$ proizvoljan, a $a_n$ je manji od $n$ i takav da je suma $a_1 + \cdots +a_n$ djeljiva s $n$.
Dokaži da niz nakon nekog člana postane konstantan, tj. postoji $k \in \mathbb{N}$ takav da je $a_m = a_k$ za svaki $m \geq k$.
Školjka 
niz takav da je 
proizvoljan, a 
je manji od 
i takav da je suma 
djeljiva s 
takav da je 
za svaki 
.