Neka je

te
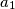
,
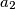
, ...,
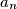
pozitivni realni brojevi za koje vrijedi
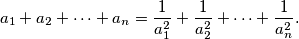
Dokaži da za svaki
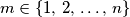
postoji

brojeva iz skupa
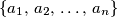
čiji je zbroj barem

.
%V0
Neka je $n \in \mathbb{N}$ te $a_{1}$, $a_{2}$, ..., $a_{n}$ pozitivni realni brojevi za koje vrijedi $$ a_{1} + a_{2} + \cdots + a_{n} = \frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + \cdots + \frac{1}{a_{n}^{2}} \text{.} $$
Dokaži da za svaki $m \in \left\{1,\,2,\,\ldots,\,n\right\}$ postoji $m$ brojeva iz skupa $\left\{a_{1},\,a_{2},\,\ldots,\,a_{n}\right\}$ čiji je zbroj barem $m$.