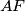
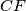
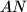
Dan je trokut , u kojem je nožište visine iz vrha . Neka su i točke na pravcu kroz različite od takve da je okomito na , a na . Neka su i polovišta i . Dokažite da je okomito na .
%V0
Dan je trokut $ABC$, u kojem je $D$ nožište visine iz vrha $A$. Neka su $E$ i $F$ točke na pravcu kroz $D$ različite od $D$ takve da je $AE$ okomito na $BE$, a $AF$ na $CF$. Neka su $M$ i $N$ polovišta $BC$ i $EF$. Dokažite da je $AN$ okomito na $MN$.
Školjka 
, u kojem je 
nožište visine iz vrha 
. Neka su 
i 
točke na pravcu kroz 
okomito na 
, a 
na 
. Neka su 
i 
polovišta 
i 
. Dokažite da je 
okomito na 
.