U ravnini je dano pet točaka
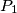
,
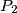
,
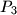
,
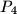
,
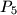
sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par
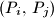
za
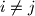
tako da pravac
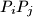
sadrži neku točku

sa cjelobrojnim koordinatama koja leži između
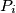
i
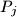
.
%V0
U ravnini je dano pet točaka $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par $(P_i,\,P_j)$ za $i \neq j$ tako da pravac $P_iP_j$ sadrži neku točku $Q$ sa cjelobrojnim koordinatama koja leži između $P_i$ i $P_j$.