Slični zadaci
a) Neka je  prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu
prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu  -tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
-tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
b) Postoji li aritmetički niz čija je razlika prirodni broj koji sadrži beskonačno mnogo kubova prirodnih brojeva, ali ne sadrži niti jedan kvadrat prirodnog broja?
 prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu
prirodni broj. Dokaži da aritmetički niz čija je razlika prirodni broj ili ne sadrži niti jednu  -tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.
-tu potenciju prirodnog broja ili ih sadrži beskonačno mnogo.b) Postoji li aritmetički niz čija je razlika prirodni broj koji sadrži beskonačno mnogo kubova prirodnih brojeva, ali ne sadrži niti jedan kvadrat prirodnog broja?
 Školjka
Školjka  prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina: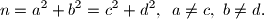
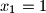 ,
, 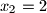 ,
, 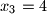 ,
, 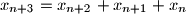 , za svako
, za svako  . Dokažite da se svaki prirodni broj može prikazati kao zbroj različitih elemenata tog niza.
. Dokažite da se svaki prirodni broj može prikazati kao zbroj različitih elemenata tog niza. 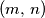 ,
, 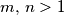 , za koje je
, za koje je 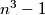 djeljivo s
djeljivo s 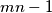 .
. 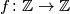 za koje vrijede sljedeća dva uvjeta:
za koje vrijede sljedeća dva uvjeta: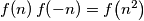 za sve
za sve 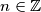
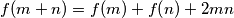 za sve
za sve 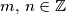 .
. 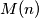 najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva
najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva 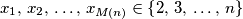 tako da vrijedi:
tako da vrijedi: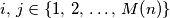 brojevi
brojevi 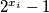 i
i 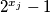 su relativno prosti.
su relativno prosti.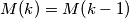 za neki prirodni broj
za neki prirodni broj  , dokaži da je
, dokaži da je 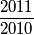 može prikazati kao umnožak dvaju razlomaka oblika
može prikazati kao umnožak dvaju razlomaka oblika 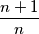 , gdje je
, gdje je