Europski matematički kup 2012. juniori 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Zadan je trokut  i točka
i točka  na simetrali kuta
na simetrali kuta  . Kružnica
. Kružnica  opisana trokutu
opisana trokutu 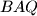 siječe stranicu
siječe stranicu  u točki
u točki 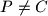 . Kružnica
. Kružnica  opisana je trokutu
opisana je trokutu 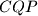 . Radijus kružnice
. Radijus kružnice  je veći od radijusa kružnice
je veći od radijusa kružnice  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 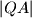 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 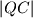 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Dokaži da je
. Dokaži da je 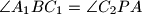 .
.
 i točka
i točka  na simetrali kuta
na simetrali kuta  . Kružnica
. Kružnica  opisana trokutu
opisana trokutu 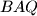 siječe stranicu
siječe stranicu  u točki
u točki 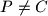 . Kružnica
. Kružnica  opisana je trokutu
opisana je trokutu 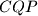 . Radijus kružnice
. Radijus kružnice  je veći od radijusa kružnice
je veći od radijusa kružnice  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 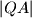 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 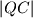 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Dokaži da je
. Dokaži da je 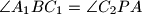 .
. Izvor: Europski matematički kup 2012. (Matija Bucić)
 Školjka
Školjka 
