Europski matematički kup 2012. seniori 2
Dodao/la:
arhiva23. prosinca 2013. Zadan je šiljastokutan trokut

i njegov ortocentar

. Dužine
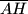
i
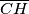
sijeku dužine

i

u točkama

i

redom. Neka je

sjecište dužina
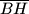
i
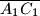
, a

polovište dužine
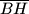
. Neka je točka
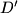
osnosimetrična slika točke

u odnosu na pravac

. Dokaži da je četverokut
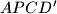
tetivan.
%V0
Zadan je šiljastokutan trokut $ABC$ i njegov ortocentar $H$. Dužine $\overline{AH}$ i $\overline{CH}$ sijeku dužine $\overline{BC}$ i $\overline{AB}$ u točkama $A_1$ i $C_1$ redom. Neka je $D$ sjecište dužina $\overline{BH}$ i $\overline{A_1C_1}$, a $P$ polovište dužine $\overline{BH}$. Neka je točka $D'$ osnosimetrična slika točke $D$ u odnosu na pravac $AC$. Dokaži da je četverokut $APCD'$ tetivan.
Izvor: Europski matematički kup 2012. (Matko Ljulj)