Europski matematički kup 2013. juniori 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Dan je trokut  i točka
i točka  unutar njega. Pravac paralelan s
unutar njega. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Pravac paralelan s
redom. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i 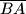 u točkama
u točkama  i
i  redom, dok pravac paralelan s
redom, dok pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Dokaži da vrijedi
redom. Dokaži da vrijedi  gdje
gdje  i
i  označavaju površinu trokuta
označavaju površinu trokuta 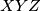 , odnosno površinu četverokuta
, odnosno površinu četverokuta  .
.
 i točka
i točka  unutar njega. Pravac paralelan s
unutar njega. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Pravac paralelan s
redom. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i 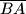 u točkama
u točkama  i
i  redom, dok pravac paralelan s
redom, dok pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Dokaži da vrijedi
redom. Dokaži da vrijedi  gdje
gdje  i
i  označavaju površinu trokuta
označavaju površinu trokuta 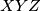 , odnosno površinu četverokuta
, odnosno površinu četverokuta  .
. Izvor: Europski matematički kup 2013. (Steve Dinh)
 Školjka
Školjka 
