Europski matematički kup 2013. juniori 4
Dodao/la:
arhiva23. prosinca 2013. Neka su

pozitivni realni brojevi takvi da je
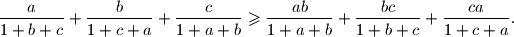
Dokaži da tada vrijedi
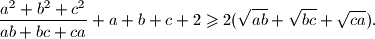
%V0
Neka su $a,b,c$ pozitivni realni brojevi takvi da je $$
\frac{a}{1+b+c} + \frac{b}{1+c+a} + \frac{c}{1+a+b} \geqslant \frac{ab}{1+a+b} + \frac{bc}{1+b+c} + \frac{ca}{1+c+a} \text{.}
$$
Dokaži da tada vrijedi $$
\frac{a^2+b^2+c^2}{ab+bc+ca}+a+b+c+2 \geqslant 2 (\sqrt{ab}+\sqrt{bc}+\sqrt{ca}) \text{.}
$$
Izvor: Europski matematički kup 2013. (Dimitar Trenevski)