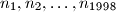
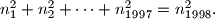
Let be positive integers such that Show that at least two of the numbers are even.
%V0
Let $ n_1, n_2, \ldots, n_{1998} $ be positive integers such that $ n_1^2 + n_2^2 + \cdots + n_{1997}^2 = n_{1998}^2. $ Show that at least two of the numbers are even.
Školjka 
be positive integers such that 
Show that at least two of the numbers are even.