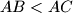
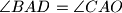
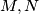
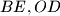
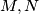
Let be an acute-angled triangle with and let be the centre of its circumcircle . Let be a point on the line segment such that . Let be the second point of intersection of and the line . If and are the midpoints of the line segments and , respectively, show that the points and are collinear.
%V0
Let $ABC$ be an acute-angled triangle with $AB<AC$ and let $O$ be the centre of its circumcircle $\omega$. Let $D$ be a point on the line segment $BC$ such that $\angle BAD = \angle CAO$. Let $E$ be the second point of intersection of $\omega$ and the line $AD$. If $M, N$ and $P$ are the midpoints of the line segments $BE, OD$ and $AC$, respectively, show that the points $M, N$ and $P$ are collinear.
Školjka 
be an acute-angled triangle with 
and let 
be the centre of its circumcircle 
. Let 
be a point on the line segment 
such that 
. Let 
be the second point of intersection of 
. If 
and 
are the midpoints of the line segments 
and 
, respectively, show that the points