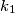
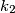
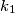
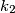
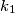
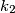
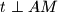
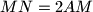
Let the circles and intersect at two points and , and let t be a common tangent of and that touches and at and respectively. If and , evaluate the angle .
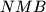
%V0
Let the circles $k_1$ and $k_2$ intersect at two points $A$ and $B$, and let t be a common tangent of $k_1$ and $k_2$ that touches $k_1$ and $k_2$ at $M$ and $N$ respectively. If $t\perp AM$ and $MN=2AM$, evaluate the angle $NMB$.
Školjka 
and 
intersect at two points 
and 
, and let t be a common tangent of 
and 
respectively. If 
and 
, evaluate the angle 
.