Let

be positive real numbers such that
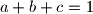
. Prove that
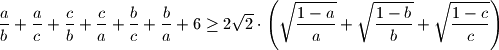
When does equality hold?
%V0
Let $a,b,c$ be positive real numbers such that $a+b+c=1$. Prove that $$
\frac{a}{b} + \frac{a}{c} + \frac{c}{b} + \frac{c}{a} + \frac{b}{c} + \frac{b}{a} + 6
\geq 2\sqrt{2} \cdot \left( \sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-b}{b}}+\sqrt{\frac{1-c}{c}} \right)
$$ When does equality hold?