Papir oblika kvadrata s vrhovima

,

,

i

ima stranica duljina

. Na njegovim stranicama
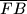
i
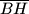
označenje su točke

i

, odnosno

i

, takve da je
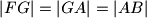
i
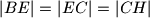
. Papir je presavinut po dužinama
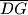
,
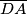
,
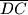
i

tako da se točka

poklopi s

, a točke

i

s točkom

. Odredite volumen tako nastale trostrane piramide

.
%V0
Papir oblika kvadrata s vrhovima $F$, $B$, $H$ i $D$ ima stranica duljina $a$. Na njegovim stranicama $\overline{FB}$ i $\overline{BH}$ označenje su točke $G$ i $A$, odnosno $E$ i $C$, takve da je $|FG| = |GA| = |AB|$ i $|BE| = |EC| = |CH|$. Papir je presavinut po dužinama $\overline{DG}$, $\overline{DA}$, $\overline{DC}$ i $\overline{AC}$ tako da se točka $G$ poklopi s $B$, a točke $F$ i $H$ s točkom $E$. Odredite volumen tako nastale trostrane piramide $ABCD$.