Neka je
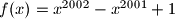
. Dokazati da su za svaki prirodan broj

brojevi

,
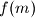
,
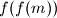
,
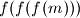
, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od

.
%V0
Neka je $f(x) = x^{2002} - x^{2001} + 1$. Dokazati da su za svaki prirodan broj $m$ brojevi $m$, $f(m)$, $f(f(m))$, $f(f(f(m)))$, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od $1$.