unutar troukta

s duljinama stranica

i odgovarajucim kutevima
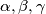
postoje tocke

i

takve da vrijedi
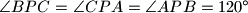
,
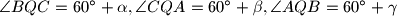
.
dokazite da vrijedi jednakost
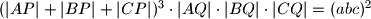
%V0
unutar troukta $ABC$ s duljinama stranica $a, b, c$ i odgovarajucim kutevima $\alpha, \beta, \gamma$ postoje tocke $P$ i $Q$ takve da vrijedi
$\angle BPC = \angle CPA = \angle APB = 120^\circ$,
$\angle BQC = 60^\circ + \alpha, \angle CQA = 60^\circ + \beta, \angle AQB = 60^\circ + \gamma$.
dokazite da vrijedi jednakost
$(|AP| + |BP| + |CP|)^3\cdot|AQ|\cdot|BQ|\cdot|CQ| = (abc)^2$