Nad stranicama
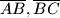
trokuta

konstruirani su kvadrati
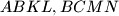
(koji s trokutom imaju samo zajednicku stranicu).
a) Ako je

tocka takva da je

paralelogram, dokazi da su trokuti

i
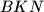
sukladni.
b) Dokazi da su polovista duzina
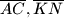
i sredista kvadrata
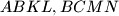
vrhovi kvadrata.
%V0
Nad stranicama $\overline{AB}, \overline{BC}$ trokuta $ABC$ konstruirani su kvadrati $ABKL, BCMN$ (koji s trokutom imaju samo zajednicku stranicu).
a) Ako je $D$ tocka takva da je $ABCD$ paralelogram, dokazi da su trokuti $ABD$ i $BKN$ sukladni.
b) Dokazi da su polovista duzina $\overline{AC}, \overline{KN}$ i sredista kvadrata $ABKL, BCMN$ vrhovi kvadrata.