neka je

polinom

-tog stupnja ciji su svi koeficijenti nenegativni, a vodeci i slobodni koeficijent jednaki su

. uz pretpostavku da su sve nultocke od

realni brojevi, dokazite da za svaki
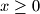
vrijedi
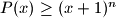
.
%V0
neka je $P$ polinom $n$-tog stupnja ciji su svi koeficijenti nenegativni, a vodeci i slobodni koeficijent jednaki su $1$. uz pretpostavku da su sve nultocke od $P$ realni brojevi, dokazite da za svaki $x \geq 0$ vrijedi $P(x) \geq (x + 1)^n$.