Slični zadaci
Dan je 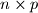 pravokutnik podijeljen na
pravokutnik podijeljen na 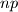 jedinicnih kvadratica. Na pocetku je
jedinicnih kvadratica. Na pocetku je  kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci
kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci  takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
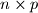 pravokutnik podijeljen na
pravokutnik podijeljen na 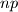 jedinicnih kvadratica. Na pocetku je
jedinicnih kvadratica. Na pocetku je  kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci
kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci  takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.  Školjka
Školjka 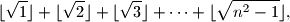 gdje je
gdje je 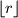 najveći cijeli broj koji nije veći od
najveći cijeli broj koji nije veći od  .
.  konveksni cetverokut i neka su
konveksni cetverokut i neka su  i
i  redom tocke na njegovim stranicama
redom tocke na njegovim stranicama  i
i  takve da je
takve da je 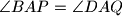 . dokazite da trokuti
. dokazite da trokuti 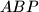 i
i 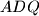 imaju jednake povrsine ako i samo ako je spojnica njihovih ortocentara okomita na pravac
imaju jednake povrsine ako i samo ako je spojnica njihovih ortocentara okomita na pravac  .
.  vrijedi nejednakost
vrijedi nejednakost![\frac{1}{\sqrt[n]{m}} + \frac{1}{\sqrt[m]{n}} > 1.](/media/m/a/4/6/a4694acdd31823c66163542e3070bae5.png)
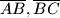 trokuta
trokuta  konstruirani su kvadrati
konstruirani su kvadrati 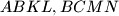 (koji s trokutom imaju samo zajednicku stranicu).
(koji s trokutom imaju samo zajednicku stranicu). tocka takva da je
tocka takva da je  i
i 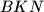 sukladni.
sukladni.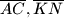 i sredista kvadrata
i sredista kvadrata 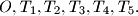 Dokazi da postoje indeksi
Dokazi da postoje indeksi 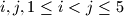 takvi da je
takvi da je 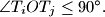
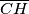 visina šiljastokutnog trokuta
visina šiljastokutnog trokuta  središte njemu opisane kružnice. Ako je
središte njemu opisane kružnice. Ako je  nožište okomice iz točke
nožište okomice iz točke  na pravac
na pravac 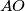 , dokaži da pravac
, dokaži da pravac 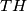 prolazi polovištem dužine
prolazi polovištem dužine