Sjecište dijagonala kvadrata

je točka

, dok je točka

polovište stranice

. Neka je

sjecište dužina

i
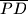
, a

sjecište dužina

i
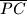
. Četverokutu
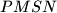
upisana je kružnica. Dokažite da je njen polumjer jednak
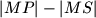
.
%V0
Sjecište dijagonala kvadrata $ABCD$ je točka $S$, dok je točka $P$ polovište stranice $\overline{AB}$. Neka je $M$ sjecište dužina $\overline{AC}$ i $\overline{PD}$, a $N$ sjecište dužina $\overline{BD}$ i $\overline{PC}$. Četverokutu $PMSN$ upisana je kružnica. Dokažite da je njen polumjer jednak $\left\vert MP \right\vert - \left\vert MS \right\vert$.