Upisana kružnica šiljastokutnog trokuta

dodiruje stranice

,

i

redom u točkama

,

i

. Središte te kružnice je točka

, a pravac
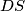
siječe dužinu
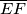
u točki

. Ako je

polovište stranice

, dokaži da su točke

,

i

kolinearne.
%V0
Upisana kružnica šiljastokutnog trokuta $ABC$ dodiruje stranice $\overline{BC}$, $\overline{CA}$ i $\overline{AB}$ redom u točkama $D$, $E$ i $F$. Središte te kružnice je točka $S$, a pravac $DS$ siječe dužinu $\overline{EF}$ u točki $P$. Ako je $M$ polovište stranice $\overline{BC}$, dokaži da su točke $A$, $P$ i $M$ kolinearne.